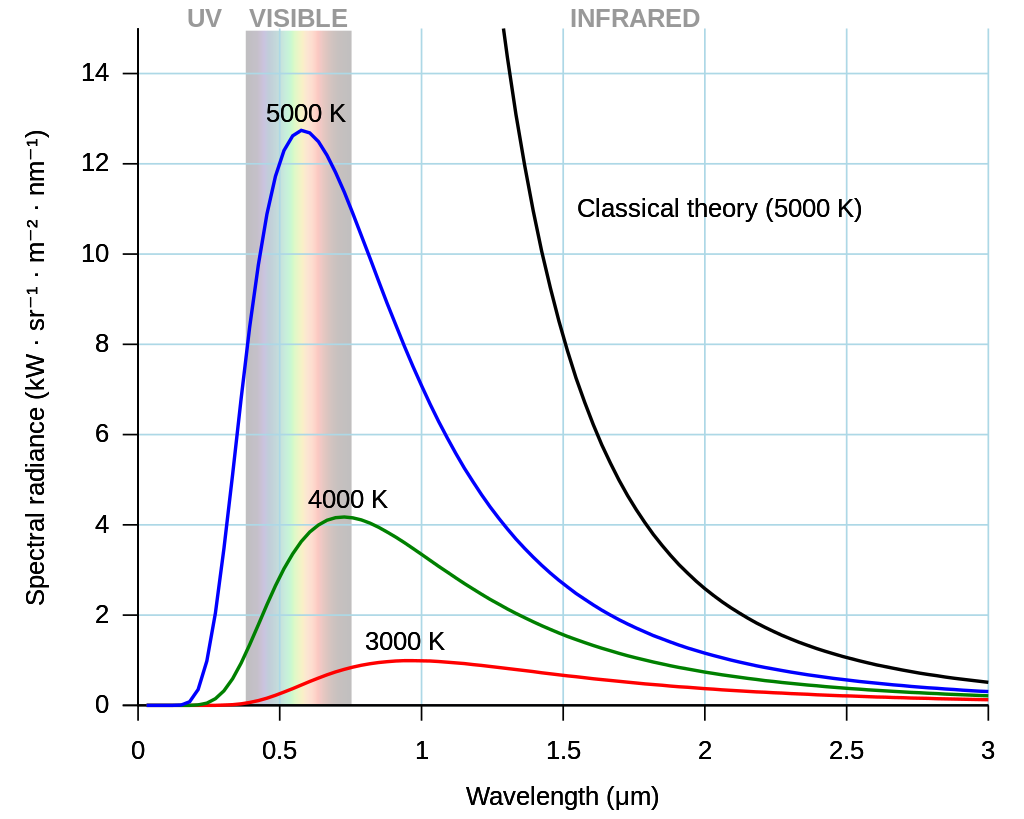
The black-body radiation graph compared with the classical model of Rayleigh and Jeans. Image from Wikipedia
Black-body (hypothetical) is any object from which electromagnetic radiation emanates solely due to the thermal motion of its charges. Any radiation that strikes it must be absorbed.
Max Plank in the year 1900 found the theory that explains black-body radiation, which resolved the problem so called ultraviolet catastrophe (Detailed discussion below. Also, see classical theory curve in picture below, which tends to infinity), and started the quantum age.

The black-body radiation graph compared with the classical model of Rayleigh and Jeans. Image from Wikipedia
The goal of the theory of black-body radiation is to find the spectral energy density $$dU=\text{ energy between }f\text{ to }f+df.$$ Let us define:$$dN(f)\equiv\text{number of modes between }f\text{ to }f+df,$$ $$\overline{E(f)}\equiv\text{average energy for a wave of freq }f.$$ We can assume$$dU\approx dN \overline{E}.$$
First let us figure out what is \(dN\), which is essentially a counting-mode problem.
Begin with considering a 1-D case: wave on a string from \(x=0\) to \(x=L\) can be represented as $$\Psi(x,t)=A\sin\left(\frac{n\pi x}{L}\right)\cos\left(2\pi ft\right),$$ here \(n\) is the number of antinodes. Wave equation $$\frac{\partial^2}{\partial t^2}\Psi(x,t)=c^2\frac{\partial^2}{\partial x^2}\Psi(x,t),$$ here \(c\) is the velocity of the wave. So $$f=\frac{cn}{2L}.$$ As the number of antinodes is same as number of modes, \(dn=dN(f)\), so $$\frac{dN(f)}{df}=\frac{dN(f)/dn}{df/dn}=\frac{2L}{c}.$$
Now extend the above situation to a 3-D case. $$\begin{align}\Psi(x,y,z,t)=A&\sin\left(\frac{n_x\pi x}{L}\right)\sin\left(\frac{n_y\pi y}{L}\right)\\&\sin\left(\frac{n_z\pi z}{L}\right)\cos\left(2\pi ft\right),\end{align}$$ $$\frac{\partial^2}{\partial t^2}\Psi(x,t)=c^2\nabla^2\Psi(x,t).$$ We obtain $$f=\frac{cn}{2L}\text{ with }n\equiv\sqrt{n_x^2+n_y^2+n_z^2}.$$ To count modes, consider a "antinode-number space", which is a octant(卦限) with axes \(n_x\), \(n_y\), and \(n_z\). Then \(n\) becomes the "radius". The differential of number of modes \(dN(f)\) at large \(n\) limit can be treat as a spherical shell of the octant with volume \(\frac{1}{8}4\pi n^2dn\). Therefore $$\frac{dN(f)}{df}=\frac{dN(f)/dn}{df/dn}=\frac{\pi n^2L}{c}.$$ In term of frequency \(f\), we have $$dN(f)=\frac{4\pi L^3}{c^3}f^2df.$$ In addition, light can have two polarization for each mode, which introduce a factor of two. The final form for density of state is thus $$\bbox[silver]{dN(f)=\frac{8\pi L^3}{c^3}f^2df}.$$
In statistical mechanics, the probability of an oscillator within an ensemble(系综) with energy \(E\) is given by $$P(E)\propto \mathrm{e}^{-E/k_BT},$$ here \(k_b\) is the Boltzmann constant. Thus the average energy can be find via $$\overline{E}=\frac{\sum EP(E)}{\sum P(E)}=\frac{\sum E\mathrm{e}^{-E/k_BT}}{\sum\mathrm{e}^{-E/k_BT}}.$$ Classically, there is no restriction on frequency (thus energy, as \(E=hf\)), the summation turns into an integration $$\overline{E}=\frac{\int_0^\infty E\mathrm{e}^{-E/k_BT}}{\int_0^\infty\mathrm{e}^{-E/k_BT}}=k_BT.$$ This result leads to the ultraviolet catastrophe, as the spectral energy density would blow up at high frequency. Max Planck solved the problem by claiming the electromagnetic radiation with frequency \(f\) is only allowed to have energy \(E=nhf\). The new average energy is $$\overline{E(f)}=\frac{\sum_{n=0}^\infty nhf\mathrm{e}^{-nhf/k_BT}}{\sum_{n=0}^\infty\mathrm{e}^{-nhf/k_BT}}=\frac{hf}{\mathrm{e}^{nhf/k_BT}-1}.$$
Classical: $$dU(f)=k_BT\frac{8\pi V}{c^3}f^2df.$$ Planck's spectral energy density: $$\bbox[silver]{dU(f)=\frac{hf}{\mathrm{e}^{nhf/k_BT}-1}\frac{8\pi V}{c^3}f^2df}.$$
Based on Planck's spectral energy density, we can derive following laws.
To find the intensity radiated by a black-body, we can integrate the spectral energy density. $$I=\int\frac{c}{4\pi}dU=\sigma T^4,$$ here \(\sigma={(2\pi^5k_B^4)}/{(15c^2h^3)}=5.670\times10^{-8}Wm^{-2}K^{-4}.\)
By solving \({\partial(dU(\lambda)}/{\partial\lambda}=0\), we can find the peak wavelength of the radiation, which turned out to be $$\lambda_{\text{peak}}T=2.897\times10^{-3}m\cdot K.$$
(Conceptual) As mentioned in the video lecture, there are only three fundamental ways to produce light, what are they?
(Hint: Quantized energy ~ photon)
(Harris) For small \(z\), \(\mathrm{e}^z\) is approximately \(1+z\)
(a) Show Planck's spectral energy density agrees with the result of classical result in the limit of small frequency.
(b) Show at high frequencies, Planck's result approaches zero.
(Harris) Show the expression of \(dU\) in terms of wavelength \(\lambda\) is $$\frac{dU}{d\lambda}=\frac{8\pi Vhc}{\mathrm{e}^{hc/\lambda k_BT}-1}\frac{1}{\lambda^5}$$.
(Hint: \(f=c/\lambda\), so \(df=-(c/\lambda^2)d\lambda\) )
Verify $$\overline{E(f)}=\frac{\sum_{n=0}^\infty nhf\mathrm{e}^{-nhf/k_BT}}{\sum_{n=0}^\infty\mathrm{e}^{-nhf/k_BT}}=\frac{hf}{\mathrm{e}^{nhf/k_BT}-1}.$$
(Hint: the denominator is a geometric series, and the numerator is the derivative of a geometric series)